힙 (Heap)
힙은 데이터에서 최댁값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리. 항상 큰 값이 상위 레벨에 있고 작은 값이 하위레벨에 있도록 한다(최대힙). 최소힙의 경우 최솟값이 맨 위 레벨에 있다.

최대힙의 구현
class BinaryMaxHeap:
def __init__(self):
# 계산 편의를 위해 0이 아닌 1번째 인덱스부터 사용한다.
self.items = [None]
def __len__(self):
# len() 연산을 가능하게 하는 매직 메서드 덮어쓰기(Override).
return len(self.items) - 1
def _percolate_up(self):
# percolate: 스며들다.
cur = len(self)
# left 라면 2*cur, right 라면 2*cur + 1 이므로 parent 는 항상 cur // 2
parent = cur // 2
while parent > 0:
if self.items[cur] > self.items[parent]:
self.items[cur], self.items[parent] = self.items[parent], self.items[cur]
cur = parent
parent = cur // 2
def _percolate_down(self, cur):
biggest = cur
left = 2 * cur
right = 2 * cur + 1
if left <= len(self) and self.items[left] > self.items[biggest]:
biggest = left
if right <= len(self) and self.items[right] > self.items[biggest]:
biggest = right
if biggest != cur:
self.items[cur], self.items[biggest] = self.items[biggest], self.items[cur]
self._percolate_down(biggest)
def insert(self, k):
self.items.append(k)
self._percolate_up()
def extract(self):
if len(self) < 1:
return None
root = self.items[1]
self.items[1] = self.items[-1]
self.items.pop()
self._percolate_down(1)
return root힙 정렬 (Heap Sort)
class BinaryMinHeap:
def __init__(self):
# 계산 편의를 위해 0이 아닌 1번째 인덱스부터 사용한다.
self.items = [None]
def __len__(self):
# len() 연산을 가능하게 하는 매직 메서드 덮어쓰기(Override).
return len(self.items) - 1
def _percolate_up(self):
# percolate: 스며들다.
cur = len(self)
# left 라면 2*cur, right 라면 2*cur + 1 이므로 parent 는 항상 cur // 2
parent = cur // 2
while parent > 0:
if self.items[cur] < self.items[parent]:
self.items[cur], self.items[parent] = self.items[parent], self.items[cur]
cur = parent
parent = cur // 2
def _percolate_down(self, cur):
smallest = cur
left = 2 * cur
right = 2 * cur + 1
if left <= len(self) and self.items[left] < self.items[smallest]:
smallest = left
if right <= len(self) and self.items[right] < self.items[smallest]:
smallest = right
if smallest != cur:
self.items[cur], self.items[smallest] = self.items[smallest], self.items[cur]
self._percolate_down(smallest)
def insert(self, k):
self.items.append(k)
self._percolate_up()
def extract(self):
if len(self) < 1:
return None
root = self.items[1]
self.items[1] = self.items[-1]
self.items.pop()
self._percolate_down(1)
return root
def sorted_by_heap(lst):
maxheap = BinaryMaxHeap()
for elem in lst:
maxheap.insert(elem)
desc = [maxheap.extract() for _ in range(len(lst))]
return list(reversed(desc))
heapq 모듈 사용법
heapq 모듈은 이진 트리(binary tree) 기반의 최소 힙(min heap) 자료구조를 제공한다.
heap[k] <= heap[2*k+1] and heap[k] <= heap[2*k+2]min heap을 사용하면 원소들이 항상 정렬된 상태로 추가되고 삭제되며, min heap에서 가장 작은값은 언제나 인덱스 0, 즉, 이진 트리의 루트에 위치한다. 내부적으로 min heap 내의 모든 원소(k)는 항상 자식 원소들(2k+1, 2k+2) 보다 크기가 작거나 같도록 원소가 추가되고 삭제된다.
1 ---> root
/ \
3 5
/ \ /
4 8 7
#위 공식을 만족시키는 간단한 min heap의 구조heapq 모듈에은 파이썬의 보통 리스트를 마치 최소 힙처럼 다룰 수 있도록 도와준다. 그래서 그냥 빈 리스트를 생성해놓은 다음 heapq 모듈의 함수를 호출할 때 마다 이 리스트를 인자로 넘겨야 한다. 즉, 파이썬에서는 heapq 모듈을 통해서 원소를 추가하거나 삭제한 리스트가 그냥 최소 힙이다.
#최소 힘 생성
heap = []
#-------------------------------------------------------------------------------
# 힙에 원소 추가 (O(logN))
heapq.heappush(heap, 4)
heapq.heappush(heap, 1)
heapq.heappush(heap, 7)
heapq.heappush(heap, 3)
>>>> heap
[1,3,7,4]
#-------------------------------------------------------------------------------
# 힙에서 원소 삭제 (O(logN))
heapq.heappop(heap)
>>>> 1
heap
>>>> [3,4,7]
#-------------------------------------------------------------------------------
# 최소값 삭제 하지 않고 얻기
# 인덱스 0에 가장 작은 원소가 있다고 해서,인덱스 1에 두번째 작은 원소,
# 인덱스 2에 세번째 작은 원소가 있다는 보장은 없다.
# 왜냐하면 힙은 heappop() 함수로 원소를 삭제할 때마다 이진 트리의 재배치한다.
heap[0]
>>>> 4
#-------------------------------------------------------------------------------
# 기존 리스트를 힙으로 변환하기
heap = [4, 1, 7, 3, 8, 5]
heapq.heapify(heap)
heap
>>>> [1, 3, 5, 4, 8, 7]
#-------------------------------------------------------------------------------
# 최대힙 (응용)
import heapq
nums = [4, 1, 7, 3, 8, 5]
heap = []
for num in nums:
heapq.heappush(heap, (-num, num)) # (우선 순위, 값)
while heap:
print(heapq.heappop(heap)[1]) # index 1
>>>>
8
7
5
4
3
1
#-------------------------------------------------------------------------------
# K번째 최소값/최대값 (응용)
def kth_smallest(nums, k):
heap = []
for num in nums:
heapq.heappush(heap, num)
kth_min = None
for _ in range(k):
kth_min = heapq.heappop(heap)
return kth_min
print(kth_smallest([4, 1, 7, 3, 8, 5], 3))
>>>> 4
#-------------------------------------------------------------------------------
# 힙 정렬 (응용)
import heapq
def heap_sort(nums):
heap = []
for num in nums:
heapq.heappush(heap, num)
sorted_nums = []
while heap:
sorted_nums.append(heapq.heappop(heap))
return sorted_nums
print(heap_sort([4, 1, 7, 3, 8, 5]))
>>>> [1, 3, 4, 5, 7, 8]이진 탐색
이진탐색이란?
- 배열이 정렬되어있을 경우, 절반씩 줄여나가면서 탐색하는 기법
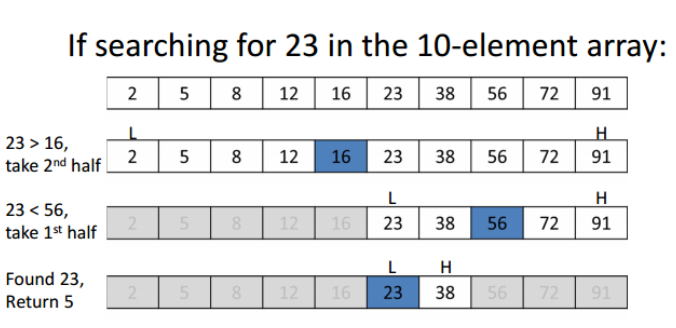
이진탐색의 효율성
- 1억 개 목록을 선형탐색할 때, 1억 번을 연산해야 한다. 이진탐색으로 찾는다면, 27번 안에 찾을 수 있다.
- import math math.log2(100000000) # 26.575424759098897
- 이진탐색을 위해서는 정렬되어 있어야 한다
이진 탐색 구현
def binary_search(nums, target):
def bs(start, end):
if start > end:
return -1
mid = (start + end) // 2
if nums[mid] < target:
return bs(mid + 1, end)
elif nums[mid] > target:
return bs(start, mid - 1)
else:
return mid
return bs(0, len(nums) - 1)
def binary_search_builtin(nums, target):
idx = bisect.bisect_left(nums, target)
# idx == len(nums) 가능하기 떄문.
"""Return the index where to insert item x in list a, assuming a is sorted.
The return value i is such that all e in a[:i] have e < x, and all e in
a[i:] have e >= x. So if x already appears in the list, a.insert(x) will
insert just before the leftmost x already there.
Optional args lo (default 0) and hi (default len(a)) bound the
slice of a to be searched.
"""
if idx < len(nums) and nums[idx] == target:
return idx
else:
return -1'TIL' 카테고리의 다른 글
| [TIL]20220531 (0) | 2022.05.31 |
|---|---|
| [TIL]20220530 (0) | 2022.05.30 |
| [TIL]20220528 (0) | 2022.05.29 |
| [TIL]20220527 (0) | 2022.05.27 |
| [TIL]20220526 (0) | 2022.05.26 |



